Today I’ve received a copy of Serious Cryptography and jumped straight ahead to Chapter 12 talking about Elliptic Curves. I’m more or less aware of how RSA works, but was intruigued for a few years now about how criptography was able to achieve same security capabilities with more efficiency while dealing with less information.
Basically that is a different kind of beast based on the hard it is to retrieve the exponent from a discrete logarithm, instead of rely on the factorization of a number composed from two large primes as it is with RSA. As the size of the numbers are much lower with the same hardness to attack, the keys involved are also way smaller.
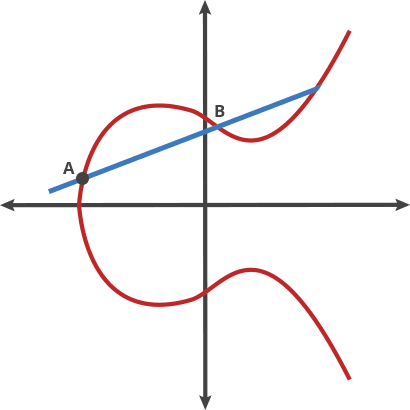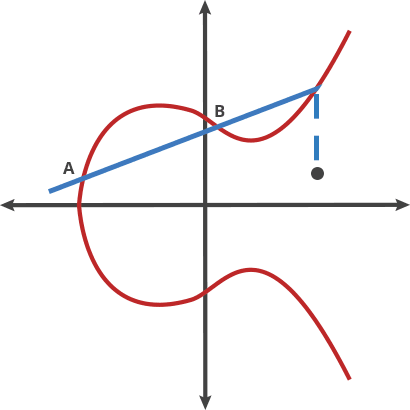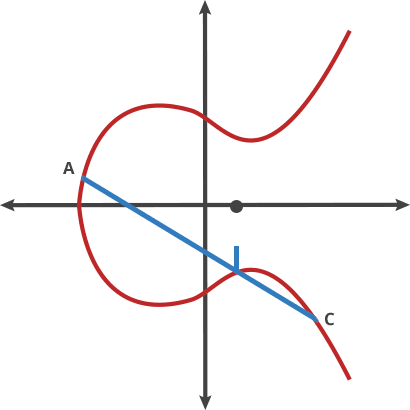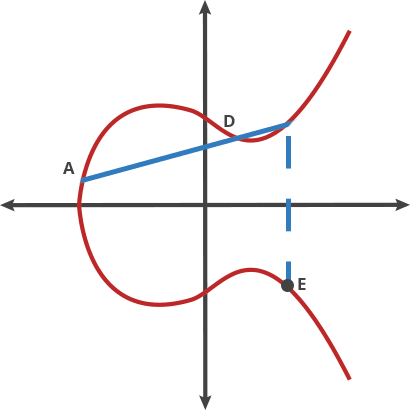
Elliptic Curve comes after the properties of the equation that the field of work is based, an equation of the curve of the type y^2=x^3 + ax + b where a and b are pre-cooked parameters that must be carefully chosen to avoid security risks.
In fact, there are two main curves used nowadays. One are a family of curves that the NIST approved, the most famous known as P-256, being the most commonly used in the industry, but also had some critisism because those a and b params in the equation were defined by the NSA and the generation is not completely publicly known. Therefore it could have potentially unknown pre-cooked attacks, althought based on the book, the general consensus by the experts is that there is no problem.
The second one is the curve generated by Daniel J. Bernstein that have pretty much the security of the NIST one and arguabilly a bit more of performance speed. It is called Curve25519 because the (discrete) field it works on is based on the prime number 2^255-19, having a=486662 and b=x .